시간복잡도와 빅오 O(N^2)는 나쁘고 O(NlogN)는 괜찮고 O(N)는 좋다

빅오표기법

빅오 표기법(Big O notation)은 알고리즘의 성능 분석을 위한 수학적인 표기법이다.

컴퓨터가 같은 계산결과를 내더라도 어떤 자료구조와 어떤 알고리즘을 사용하는가에 따라 계산시간이 달라진다.피보나치 수열을 구하는 알고리즘을 보자. 두개의 알고리즘의 실행시간은 계산횟수를 통해 유추해볼 수 있다.

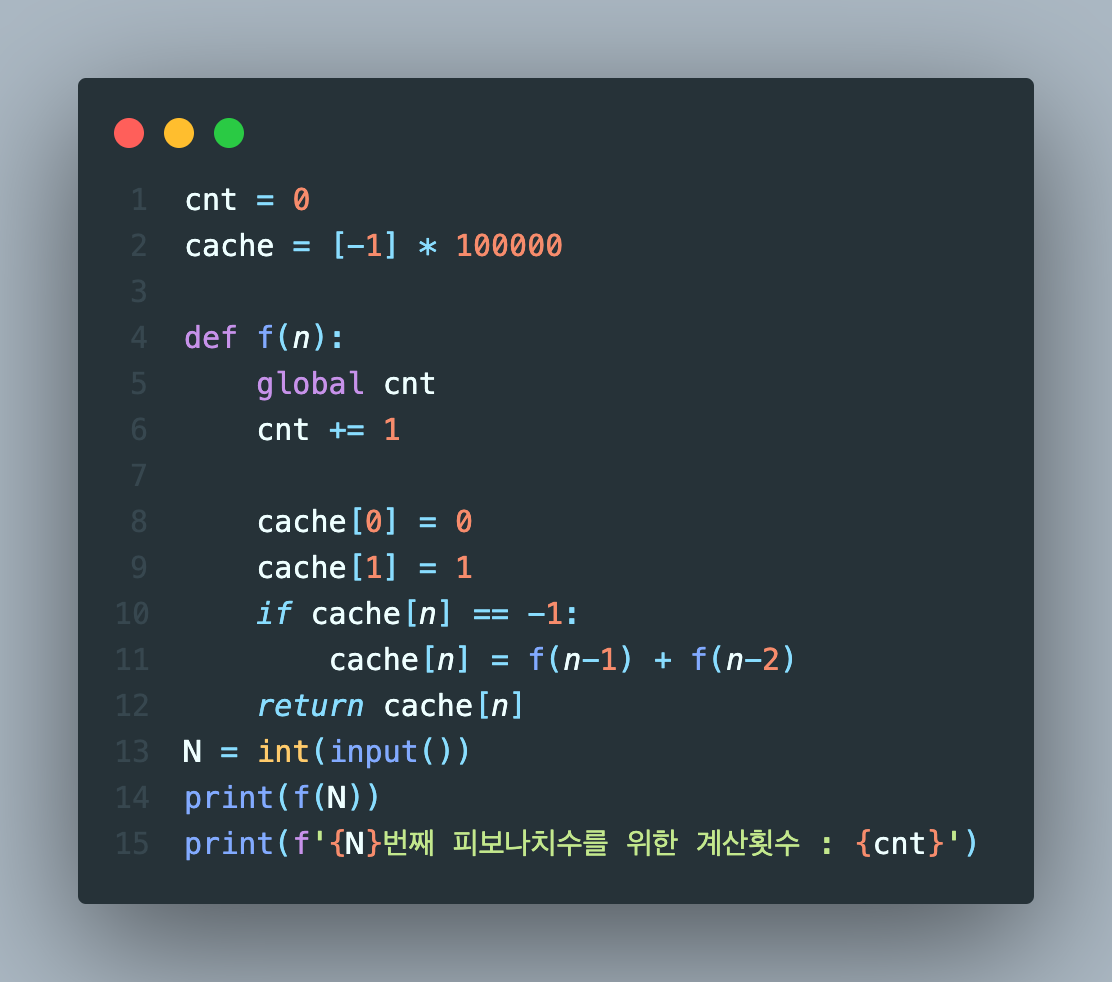
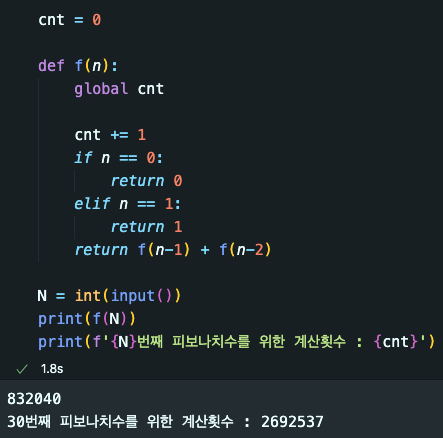
if문의 경우 시간복잡도도 O(1)이고 덧셈의 시간복잡도도 O(1)여서 함수한번 호출하는데에는 시간복잡도가 O(1)지만 함수 호출 횟수가 많아질 경우 프로그램 실행속도가 급격하게 느려진다.

하지만 cache라는 리스트를 도입해서 값을 임시저장해놓으면 계산횟수가 획기적으로 줄어든다.

일반적으로 코딩테스트의 실행시간 제한은 1~2초이고 1억까지는 1~2초안에 실행된다고 한다. 오른쪽의 경우 30번째 까지는 그나마 통과할 수 있겠지만 N이 40만 되어도 33억회의 계산횟수가 필요하게 되고 아무리 O(1)이어도 O(1)*33억 ~ 33억 이상 이기 때문에 통과하지 못하게 된다. 실제 실행시간도 34초정도로 매우 느리게 실행되는것을 확인할 수 있다. 

O(N^2)은 나쁘고 O(NlogN)은 괜찮고 O(1)는 좋다

그래프에서 볼 수 있듯 O(N^2)은 N이 조금만 커져도 시간복잡도가 급격하게 커진다.

for 문의 경우 시간복잡도는 O(N)이다. 하지만 for문이 들어간 함수를 N번 실행해야 답을 찾는다면 O(N) * N으로 전체계산복잡도는 O(N^2) 되어버린다. 그냥 프로그램 구현하는 것만으로도 벅찬데.. 이걸 어떻게 신경쓰지.. 싶지만 그나마 문제별로 적용하는 최선의 알고리즘이 유형화되어있기 때문에.. 그냥 외우자..

대표적인 알고리즘별 시간복잡도

시간복잡도 Big O	대표적인 알고리즘
O(1)	단순대입, 덧셈, 뺄셈, 비교, 할당, IF문 append(맨 뒤에 삽입), heappush(힙삽입), pop(삭제), popleft(삭제)
O(log N)	이진탐색, 분할정복알고리즘
O(N)	선형탐색, for문, 리스트에서의 삽입, 삭제
O(N log N)	힙정렬, 퀵정렬
O (N^2)	버블 정렬(최악의 경우), 선택 정렬(최악의 경우), 삽입 정렬(최악의 경우), 퀵 정렬(최악의 경우), 셸 정렬
O(N^3)	행렬곱셈
O(2^N)	하노이의 탑
O(N!)	외판원문제, 순열생성

대표적으로는 이렇게 되어있는데 반복문이나 호출횟수 등에 의해 더 많아질 수 있다.